笔记|生成模型(三):生成对抗理论
生成对抗网络(Generative Adversarial Nets,GAN)
核心思想
生成对抗网络是一种基于对抗学习的深度生成模型,最早由Ian Goodfellow于2014年在《Generative Adversarial Nets》中提出,一经提出便成为了学术界研究的热点,也将生成模型的热度推向了另一个新的高峰。上节有讨论到,直接用图片做监督存带来均值灾难,我们又无法得到真实分布从而监督训练。因此,借助变分推断的思想做一个概率分布近似。从一个简单的已知分布(如标准高斯分布)出发,通过某种方式或手段,将其近似为真实数据的概率分布。GAN正是遵循这一理论,但实现过程中直接对齐分布是很难的,因为我们并不知道概率分布的函数形式,所以也无法得知它到底有几个参数。
所以可以换一个思想,既然无法得到概率分布函数的具体形式,没有参数,不好近似,那我就不去近似他了。对于两个分布而言,如果它们的大多数随机采样的样本概率都是对齐的,那不就说明这两个概率分布函数已经接近了吗。很好,你已经掌握了生成对抗网络的要领,试着自己实现一下吧。(-_-||)
网络架构
生成对抗网络采用双网络架构设计,由生成器(Generator, G)和判别器(Discriminator, D)两个神经网络组成,它们在训练过程中相互对抗、共同进化。
生成器网络:作为整个系统的"创造者",生成器的任务是学习从简单的噪声分布(通常是标准高斯分布)到复杂数据分布的映射关系。具体而言,它接收一个低维的随机噪声向量 \(z \sim p_z(z)\) 作为输入,通过多层神经网络的非线性变换,输出与真实数据维度相同的生成样本 \(G(z)\)。生成器的目标是使生成的样本在分布上尽可能接近真实数据分布 \(p_{data}(x)\)。
判别器网络:作为系统的"鉴别专家",判别器本质上是一个二分类器。它接收来自两个不同源的样本——真实数据集中的样本 \(x \sim p_{data}(x)\) 和生成器产生的样本 \(G(z)\),输出一个概率值 \(D(x) \in [0,1]\),表示输入样本来自真实数据分布的概率。判别器的目标是最大化正确分类的概率:对真实样本输出接近1,对生成样本输出接近0。
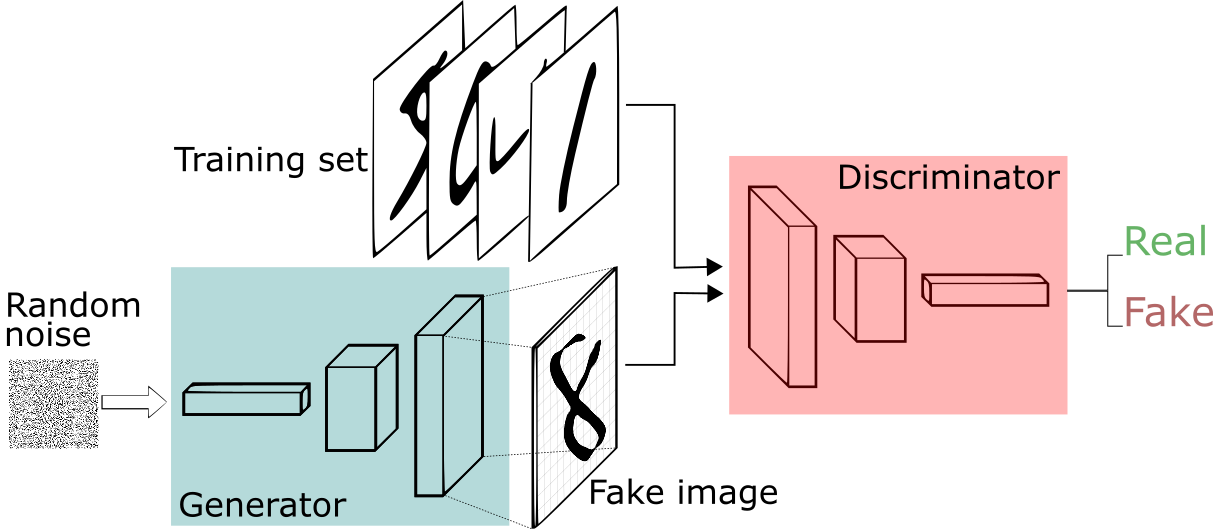
这种架构设计的巧妙之处在于,通过样本对齐来实现分布对齐。如果生成器产生的样本能够骗过判别器,说明生成分布已经在某种程度上接近了真实分布,而无需显式地建模分布函数。随着训练的进行,两个网络在对抗中相互提升,最终达到一个动态平衡状态。实现了样本概率之间的对齐,而不是样本对齐。(上一节说了直接图像对齐带来均值灾难,其本质原因是训练过程对齐的是样本而不是样本的概率)
对抗训练机制
GAN 的损失函数核心思想在于 对抗训练,生成器 G 和判别器 D 进行一场零和博弈:
- 生成器(Generator):试图生成足以 "以假乱真"
的样本,欺骗判别器
- 判别器(Discriminator):试图准确区分真实样本和生成样本
这种对抗关系可以用一个形象的比喻来理解:生成器就像一个造假币的人,而判别器就像一个验钞机。造假者不断提高造假技术,而验钞机也在不断提升鉴别能力。在这个博弈过程中,两者的能力都在不断提升。论文所述训练步骤如图所示。

训练步骤
首先,使用交叉熵损失函数来训练判别器参数 \(\theta_d\)。从高斯分布 \(p_g(z)\) 中采样 \(m\) 个噪声向量:\(\{ z^{(1)}, \ldots, z^{(m)} \}\)。从数据分布 \(p_{\text{data}}(x)\) 中采样 \(m\) 个真实样本:\(\{ x^{(1)}, \ldots, x^{(m)} \}\)。使用交叉熵损失训练判别器网络 \(\theta_d\):
\[ \mathop{\arg\min}_{\theta_d} \left( \frac{1}{m} \sum_{i=1}^{m} \left[ \log D(x^{(i)}) + \log \left( 1 - D(G(z^{(i)})) \right) \right] \right) \]
从损失函数可以看出,目标是使 \(\log D(x^{(i)})\) 趋于 1,\(D(G(z^{(i)}))\) 趋于 0,以达到判别器识别生成数据的目的。
判别器更新后,固定判别器参数。重新再次采样 \(m\) 个噪声向量:\(\{ z^{(1)}, \ldots, z^{(m)} \}\)。最小化判别损失以使生成器能够骗过判别器(即让生成的样本更像真实样本):
\[ \mathop{\arg\min}_{\theta_g} \left( \frac{1}{m} \sum_{i=1}^{m} \left[ \log \left( 1 - D(G(z^{(i)})) \right) \right] \right) \]
💡 在实际应用中,为了提升生成器的梯度,也常使用替代形式:\(-\log(D(G(z)))\),其目标是让判别器认为生成样本为真。
重复以上步骤,直到判别器和生成器都收敛。
最后,整个训练的损失函数可以整合为对抗损失函数(Adversarial Loss Function / Minimax Objective)
\[ \min_G \max_D \; V(D, G) = \mathbb{E}_{x \sim p_{\text{data}}(x)} \left[ \log D(x) \right] + \mathbb{E}_{z \sim p_g(z)} \left[ \log \left( 1 - D(G(z)) \right) \right] \]
其中:
- \(D(x)\) 表示判别器对真实样本 \(x\) 判定为真的概率;
- \(D(G(z))\) 表示判别器对生成样本为真的概率;
- \(G(z)\) 是生成器对输入噪声 \(z\) 的映射输出;
- \(\mathbb{E}_{x \sim p_{\text{data}}(x)}\) 是对真实数据分布的期望;
- \(\mathbb{E}_{z \sim p_g(z)}\) 是对生成器输入噪声分布的期望。
GAN能达到平衡背后的数学证明
在理想情况下,当训练达到纳什均衡时:
- 判别器无法区分真假样本,即 \(D(x) = 0.5\)
- 生成器的生成分布与真实数据分布一致,即 \(p_g = p_{data}\)
从理论上可以证明,在最优判别器的情况下,生成器的优化目标等价于最小化生成分布与真实分布之间的JS散度(Jensen-Shannon Divergence)。 JS散度与KL散度的定义
详细证明
步骤1:求解最优判别器
对于固定的生成器G,判别器D的目标是最大化: \[V(G,D) = \int_x p_{data}(x)\log D(x)dx + \int_z p_z(z)\log(1-D(G(z)))dz\]
由于 \(p_g(x) = \int_z p_z(z)\delta(x-G(z))dz\),可以重写为: \[V(G,D) = \int_x p_{data}(x)\log D(x) + p_g(x)\log(1-D(x))dx\]
对于任意固定的x,最优的D(x)应该最大化: \[f(D) = p_{data}(x)\log D(x) + p_g(x)\log(1-D(x))\]
对D求导并令其为0: \[\frac{\partial f}{\partial D} = \frac{p_{data}(x)}{D(x)} - \frac{p_g(x)}{1-D(x)} = 0\]
解得最优判别器: \[D^*_G(x) = \frac{p_{data}(x)}{p_{data}(x) + p_g(x)}\]
步骤2:将最优判别器代入目标函数
将 \(D^*_G(x)\) 代入原始目标函数: \[C(G) = \max_D V(G,D) = V(G,D^*_G)\]
\[= \mathbb{E}_{x\sim p_{data}}\left[\log\frac{p_{data}(x)}{p_{data}(x) + p_g(x)}\right] + \mathbb{E}_{x\sim p_g}\left[\log\frac{p_g(x)}{p_{data}(x) + p_g(x)}\right]\]
步骤3:变换为JS散度
注意到: \[\log\frac{p_{data}(x)}{p_{data}(x) + p_g(x)} = \log\frac{p_{data}(x)}{2 \cdot \frac{p_{data}(x) + p_g(x)}{2}} = \log\frac{p_{data}(x)}{2M(x)} = \log 2 + \log\frac{p_{data}(x)}{M(x)}\]
其中 \(M(x) = \frac{p_{data}(x) + p_g(x)}{2}\) 是两个分布的平均。
因此: \[C(G) = \log 4 + KL(p_{data} \| M) + KL(p_g \| M)\]
根据JS散度的定义: \[JS(p_{data} \| p_g) = \frac{1}{2}KL(p_{data} \| M) + \frac{1}{2}KL(p_g \| M)\]
我们得到: \[C(G) = \log 4 + 2 \cdot JS(p_{data} \| p_g)\]
步骤4:生成器的优化目标
由于生成器G要最小化 \(C(G)\),而 \(\log 4\) 是常数,因此: \[\min_G C(G) \Leftrightarrow \min_G JS(p_{data} \| p_g)\]
关键洞察:
- 当且仅当 \(p_g = p_{data}\) 时,JS散度为0,达到全局最小值
- 此时最优判别器 \(D^*_G(x) = \frac{1}{2}\),无法区分真假样本
- 这证明了GAN在理论上能够学习到真实数据分布
这个证明揭示了几个重要事实:
- GAN隐式地最小化JS散度:虽然我们没有显式计算两个分布之间的距离,但通过对抗训练,实际上在最小化JS散度
- 判别器的作用:判别器不仅仅是一个分类器,它实际上在估计两个分布的密度比
- 收敛性保证:在理想条件下(无限容量、充分训练),GAN能够收敛到真实数据分布
然而,这个理论分析基于几个理想假设(如无限容量的模型、全局最优等),在实践中可能难以满足,这也是GAN训练不稳定的原因之一。
GAN的优势与挑战
优势: 1. 无需显式建模概率密度:不需要像VAE那样引入变分下界 2. 生成质量高:能够生成非常逼真的样本 3. 理论优雅:基于博弈论的框架简洁而有力
挑战: 1. 训练不稳定:生成器和判别器的平衡很难把握 2. 模式坍塌(Mode Collapse):生成器可能只学会生成某几种模式的样本 3. 梯度消失:当判别器过于强大时,生成器的梯度会消失 4. 评估困难:难以定量评估生成模型的质量
GAN的变体与改进
为了解决原始GAN的问题,研究者们提出了许多改进版本:
- DCGAN(Deep Convolutional GAN):使用卷积神经网络架构,提高了训练稳定性
- WGAN(Wasserstein GAN):使用Wasserstein距离替代JS散度,缓解了梯度消失问题
- LSGAN(Least Squares GAN):使用最小二乘损失,使生成样本更接近决策边界
- StyleGAN:引入风格控制,实现了高质量、可控的图像生成
- CycleGAN:实现了无配对数据的图像到图像转换
总结
GAN开创了生成模型的新时代,通过对抗学习的思想,巧妙地避开了直接建模概率分布的困难。虽然训练过程存在诸多挑战,但其强大的生成能力使其在图像生成、风格迁移、超分辨率等多个领域取得了巨大成功。随着各种改进技术的出现,GAN已经成为深度学习中最重要的生成模型之一。
